CSapp-Chapter2

Computer System A Programmers Perspective This book is written from a programmer's perspective which describes how application programmers can use their knowledge of a system to write better programs.

---

Chapter 2

---

Pre

• Unsigned encodings are based on traditional binary notation, representing numbers greater than or equal to 0.
• Two’s-complement encodings are the most common way to represent signed integers, that is, numbers that may be either positive or negative.
• Floating-point encodings are a base-two version of scientific notation for
  representing real numbers.

---

2.1 Information Storage

Hexadecimal Notation

Numeric constants starting with 0x or 0X are interpreted as being in hexadecimal, (or simply “hex”).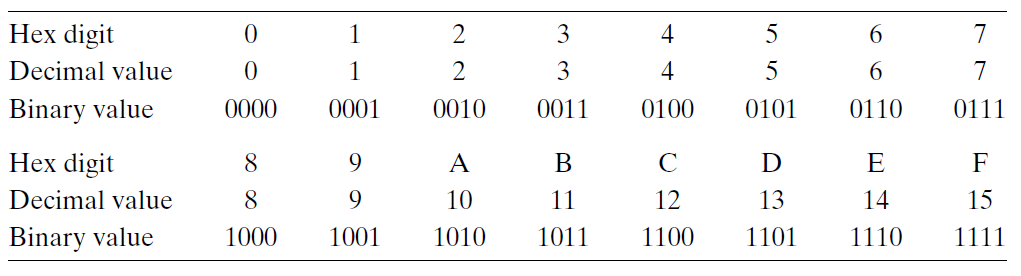

Words

for a machine with a w-bit word size, the virtual addresses can range from 0 to 2w − 1, giving the program access to at most 2w bytes.

Addressing and Byte Ordering

_Little endian_： The former convention—where the least significant byte comes first.(This convention is followed by most Intel-compatible machines.)
Big endian: The latter convention—where the most significant byte comes first.
Supposing the variable x of type int and at address 0x100 has a hexadecimal value of 0x01234567.(This convention is followed by most machines from IBM and Sun Microsystems.)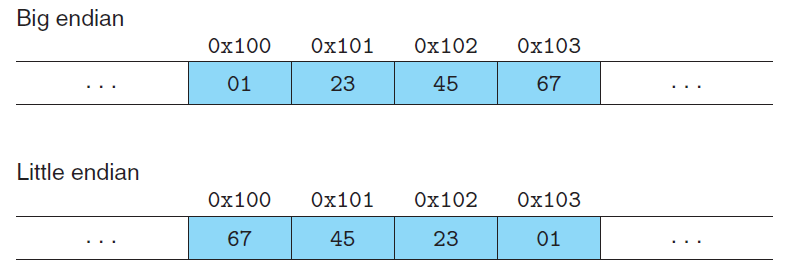

Story:In fact, the terms “little endian” and “big endian” come from the book Gulliver’s Travels by Jonathan Swift, where two warring factions could not agree as to how a soft-boiled egg should be opened—by the little end or by the big.

Bit-Level Operations in C

As an application of the property that a ^ a = 0 for any bit vector a, consider the following program:

void inplace_swap(int *x, int *y){
    *y = *x ^ *y;
    *x = *x ^ *y;
    *y = *x ^ *y;
}

void reverse_array(int a[], int length)
{
    int first, last;

    for (first = 0, last = length-1; first<last; first++, last--)
        inplace_swap(&a[first], &a[last]);

    for (first=0; first<length; first++)
        printf("%d", a[first]);
    printf("\n");
}

Steps	x	y
initialization	0100 0001	0101 1001
Steps 1	0100 0001	0001 1000
Steps 2	0101 1001	0001 1000
Steps 3	0101 1001	0100 0001

---

2.2 Integer Representations

Unsigned Encodings

$B2U_{w}$(for “binary to unsigned,” length w):

$B2U_{w}(\vec{x})\doteq\sum_{i=0}^{w-1}x_{i}2^i$

Two’s-Complement Encodings

$B2T_{w}$ (for “binary to two’s-complement” length w):

$B2T_{w}(\vec{x})\doteq-x_{w-1}2^{w-1}+\sum_{i=0}^{w-2}x_{i}2^i$

Signed vs. Unsigned in C

Although the C standard does not specify a particular representation of signed numbers, almost all machines use two’s complement. Generally, most numbers are signed by default. For example, when declaring a constant such as 12345 or 0x1A2B, the value is considered signed. Adding character ‘U’ or ‘u’ as a suffix creates an unsigned constant, e.g., 12345U or 0x1A2Bu.

When an operation is performed where one operand is signed and the other is unsigned, C implicitly casts the signed argument to unsigned and performs the operations assuming
the numbers are nonnegative.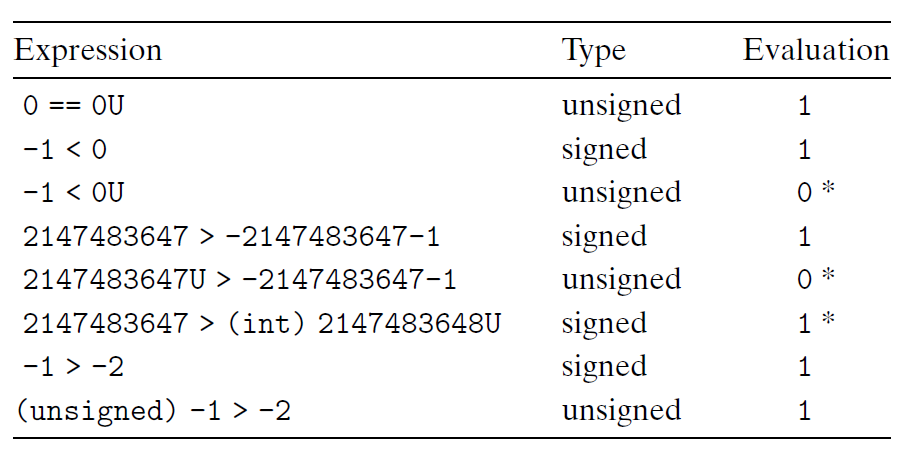

Expanding the Bit Representation of a Number

To convert an unsigned number to a larger data type, we can simply add leading zeros to the representation; this operation is known as zero extension$[x_{w-1},x_{w-2},\cdots,x_{0}]$. For converting a two’scomplement number to a larger data type, the rule is to perform a sign extension, adding copies of the most significant bit to the representation $[x_{w-1},\cdots,x_{w-1},x_{w-1},x_{w-2},\cdots,x_{0}]$.

As an example, consider the following code:

short sx = -12345; /* -12345 */
unsigned short usx = sx; /* 53191 */
int x = sx; /* -12345 */
unsigned ux = usx; /* 53191 */

printf("sx = %d:\t", sx);
show_bytes((byte_pointer) &sx, sizeof(short));
printf("usx = %u:\t", usx);
show_bytes((byte_pointer) &usx, sizeof(unsigned short));
printf("x = %d:\t", x);
show_bytes((byte_pointer) &x, sizeof(int));
printf("ux = %u:\t", ux);
show_bytes((byte_pointer) &ux, sizeof(unsigned));

//output
sx = -12345: cf c7
usx = 53191: cf c7
x = -12345: ff ff cf c7
ux = 53191: 00 00 cf c7

---

2.3 Integer Arithmetic

Abelian Group:

A mathematical structure of Modular Addition.

$$
-_{w}^ux = \begin{cases}
x,& x=0 \\
2^w-x,& x>0 \\
\end{cases}
$$

To be continued…